マージ過程を表す木
マージ過程を表す木を用いる典型テクを学んだので紹介する。
マージ過程を表す木とは
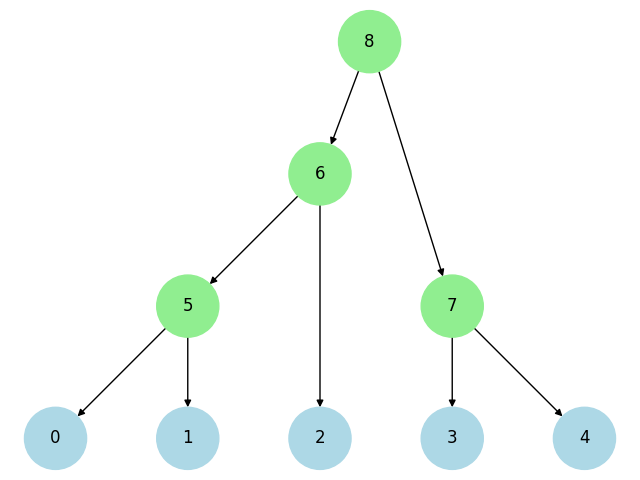
頂点$0,\dots,N-1$からなる$N$頂点$0$辺のグラフについて、指定された頂点のペアに辺を貼り連結成分をマージしていく操作を考える。各時点での連結成分に関するなんらかの値を求めたい場合や、ある頂点のペアが初めて連結になった時点での何らかの情報を得たい場合マージ過程を表す木が役に立つ可能性がある。マージ過程を表す木ではマージの途中状態を根つき森として管理する。頂点$u,v$に辺を張るというクエリに対して、仮想的な頂点$p$を追加し、$p$を根、$u,v$のそれぞれの元の根を子とするようにグラフを変形する。ただし元々$u,v$が同じ連結成分に属する場合は何もしない。$i$番目に追加される頂点のインデックスを$N+i$とすると便利である。$5$頂点のグラフに対して$(0,1),(1,2),(3,4),(0,4) $とマージを行った場合のマージ過程を表す木は次のようになる。水色の頂点が実際の頂点、緑色の頂点がマージに対応している。
最終的に連結になる場合、頂点$2N-2$を根とする頂点数$2N-1$の根付き木となる。$i$番目のマージによってできる連結成分は、マージ過程を表す木における頂点$N+i$の部分木(の葉)に対応する。このような性質のため入力で与えられるグラフが最終的に連結にならない場合も適当に辺を増やして連結にさせると便利な場合もある。
実際に問題を見ながらこの方法の使い方を見ていこう。
ABC314 F - A Certain Game
問題概要
$N$人のプレーヤーが$N-1$回のチーム戦を行う。最初$1$人からなるチームである。各試合では両チームの人数の和に対する自チームの人数の割合が勝率となり、試合後チームは合併される。$i$回目の試合では人$p_i$を含むチームと人$q_i$を含むチームが戦う。各プレーヤーについて勝つ回数の期待値を求めよ。
解法
各試合で集合のマージが行われ、試合前の各プレーヤーの属する連結成分数に応じた勝率をそれぞれの部分木に加算していく問題となる。マージ過程を表す木を作ることによりサイズをボトムアップに、勝率をトップダウンに計算することができる。
コード
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include "template.hpp"
#include "data_structure/union-find.hpp"
#include <atcoder/modint>
using mint = atcoder::modint998244353;
template <class T>
pair<vector<vector<T>>, vector<T>>
tree_of_merging_process(int n, vector<pair<T, T>> &edges) {
vector<vector<T>> res(2 * n - 1);
vector<T> par(2 * n - 1);
iota(begin(par), end(par), 0);
UnionFind dsu(n);
int aux = n; // マージする際親とする仮の頂点
for(auto [i, j] : edges) {
i = dsu.leader(i), j = dsu.leader(j);
if(i == j)
continue;
res[aux].emplace_back(par[i]);
res[aux].emplace_back(par[j]);
par[dsu.merge(i, j)] = aux++;
}
rep(i, n, 2 * n - 1) for(auto j : res[i]) par[j] = i;
return {res, par};
}
void solve() {
INT(n);
vector<pair<int, int>> edges(n);
rep(i, n - 1) {
INT(p, q);
edges[i] = {--p, --q};
}
auto [g, par] = tree_of_merging_process(n, edges);
vector<int> sz(2 * n - 1, 1);
rep(i, n, 2 * n - 1) {
sz[i] = 0;
for(auto j : g[i])
sz[i] += sz[j];
}
vector<mint> ans(2 * n - 1, 0);
for(int i = 2 * n - 3; i >= 0; i--) {
ans[i] += mint(sz[i]) / sz[par[i]];
for(auto j : g[i])
ans[j] += ans[i];
}
rep(i, n) cout << ans[i].val() << " \n"[i + 1 == n];
}
int main() {
ios::sync_with_stdio(false);
std::cin.tie(nullptr);
solve();
}
CF 683 Div.1 D. Graph and Queries
問題概要
$n$頂点$m$辺の無向グラフがある。各頂点$i$には整数$p_i$が書かれていて、$p$は$1$から$n$の順列である。 以下の2種類のクエリを $q$回処理する:
1 v— 頂点 $v$ と連結な頂点の中で、最大の値 $p_u$ を持つ頂点 $u$ を見つけ、$p_u$ を出力した後、$p_u$ を $0$ に置き換える。2 i— $i$ 番目の辺を削除する。
※$p$は互いに異なるから答えは一意に定まる
解法
辺は削除のみ行われるが、クエリを後ろから見ることにより追加の問題にできる。ただし後ろから考えた場合どの頂点が$0$に書き換えられたかがわからない。すなわちクエリ$1$は前から、クエリ$2$は後ろから見るのが都合が良い。クエリ$2$を後ろから見ることで、マージ過程を表す木を作る。これによりあるマージでできる連結成分がマージに対応する頂点の部分木になる。オイラーツアーを考えることで部分木を列の区間に対応させられる。区間に対する最大値と最大値を与えるインデックスの取得、及びその更新はセグメント木を用いることで可能である。
コード
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
#include "data_structure/segtree.hpp"
#include "tree/euler-tour.hpp"
#include <atcoder/dsu>
P op(P p, P q) {
return p.first > q.first ? p : q;
}
P e() {
return {-1, -1};
}
void solve() {
INT(n, m, q);
vector<int> p(n);
input(p);
vector<int> a(m), b(m);
rep(i, m) {
input(a[i], b[i]);
--a[i], --b[i];
}
atcoder::dsu dsu(2 * n);
vl par(2 * n);
vll chil(2 * n);
iota(all(par), 0);
ll cur = n;
vector<P> qs(q);
vector<bool> not_q(m, true);
rep(i, q) {
LL(flag, v);
--v;
qs[i] = P(flag, v);
if(flag == 2)
not_q[v] = false;
}
auto merge = [&](int id) {
ll x = dsu.leader(a[id]), y = dsu.leader(b[id]);
if(x == y)
return;
chil[cur].push_back(par[x]);
chil[cur].push_back(par[y]);
par[x] = par[y] = cur++;
dsu.merge(x, y);
};
rep(i, m) if(not_q[i]) {
merge(i);
}
for(int i = q - 1; i; i--) {
auto [flag, v] = qs[i];
if(flag == 1) {
qs[i].first = par[dsu.leader(v)];
} else {
qs[i].first = -1;
merge(qs[i].second);
}
}
rep(i, n) {
chil[cur].push_back(par[dsu.leader(i)]);
}
ranges::sort(chil[cur]);
chil[cur].erase(unique(all(chil[cur])), end(chil[cur]));
EulerTour et(chil, cur);
segtree<P, op, e> seg(et.out[cur]);
rep(i, n) {
seg.set(et.in[i], {p[i], et.in[i]});
}
rep(i, q) {
if(qs[i].first == -1)
continue;
ll time = qs[i].first;
auto val = seg.prod(et.in[time], et.out[time]);
print(max(0ll, val.first));
if(val.second != -1)
seg.set(val.second, e());
}
}
int main() {
ios::sync_with_stdio(false);
std::cin.tie(nullptr);
cout << std::setprecision(16);
solve();
}
ABC394 G - Dense Buildings
問題概要
$H\times W$に仕切られた区画がある。上から$i$番目、左から$j$番目の区画には$F_{i,j}$階建てのビルがある。ビルのある階にいるとき、次の移動ができる。
- 同じビルの1つ上または下の階に階段を使って移動する
- 上下左右に隣り合うビルの同じ階に移動する
但し存在しない階には移動できない。 $Q$個のクエリに答えよ。
区画$(A,B)$にあるビルの$Y$階から区画$(C,D)$にあるビルの$Z$階に移動するとき、階段を使う回数の最小値を求めよ。
解法
区画$(A,B)$のビルの$F_{A,B}$階から区画$(C,D)$のビルの$F_{C,D}$階に移動する際に通る階数の最小値の最大値を$M_{(A,B),(C,D)}$とする。$(A,B)$の$Y$階から$(C,D)$の$Z$階へ移動するには$X=$$\min(Y,Z,M_{(A,B),(C,D)})$階を通る必要があり、逆に$Y+Z-2X$回階段を使うことで移動できることが分かる。
従って任意のビル間について上記の$M$を求められればよいが、これは次のように可能である。初め全てのビルは独立であるとする。そしてすべての隣り合うビルのペア$i,j$について$\min(F_i,F_j)$が大きい順にビル$i,j$をマージしていき、マージ過程を表す木を作成する。ここで$i,j$のマージに対応する仮想的な頂点に重み$\min(F_i,F_j)$をもたせる。このとき、任意の(隣り合うとは限らない)ビル$i,j$について$M_{i,j}$はマージ過程を表す木における頂点$i,j$のLCAの重みと一致する。LCAはオイラーツアーとRMQなどで求められる。従って問題が解けた。
コード
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include "data_structure/union-find.hpp"
#include "template.hpp"
#include "tree/euler-tour.hpp"
void solve() {
INT(h, w);
int n = h * w;
vector<int> f(2 * n - 1);
using T = tuple<int, int, int>;
vector<T> edge;
rep(i, h) {
rep(j, w) {
int cur = i * w + j;
cin >> f[cur];
if(i)
edge.emplace_back(min(f[cur - w], f[cur]), cur - w, cur);
if(j)
edge.emplace_back(min(f[cur - 1], f[cur]), cur - 1, cur);
}
}
ranges::sort(edge, greater<T>());
vector chil(2 * n - 1, vector<int>());
vector<int> par(2 * n - 1);
iota(begin(par), end(par), 0);
UnionFind uf(n);
int aux = n;
for(auto [c, i, j] : edge) {
i = uf.leader(i), j = uf.leader(j);
if(i == j)
continue;
f[aux] = c;
chil[aux].emplace_back(par[i]);
chil[aux].emplace_back(par[j]);
par[uf.merge(i, j)] = aux++;
}
EulerTour et(chil, aux - 1);
INT(q);
rep(i, q) {
INT(a, b, y, c, d, z);
--a, --b, --c, --d;
int lca = et.lca(a * w + b, c * w + d);
int mini = min({y, z, f[lca]});
print(y + z - 2 * mini);
}
}
int main() {
ios::sync_with_stdio(false);
std::cin.tie(nullptr);
solve();
}
yukicoder No.1054 Union add query
問題概要
$N$頂点$0$辺のグラフがあり、各頂点に$0$が書かれている。$3$種類のクエリを処理せよ。
- 頂点$A,B$間に辺を張る
- 頂点$A$の連結成分内のすべての頂点に$B$を加算
- 頂点$A$に書かれた数を出力
解法
UnionFindを改造するのが楽だが、マージ過程を表す木を用いても解ける。まず、いつも通り$1$つ目のクエリについてマージ過程を表す木を作る。オイラーツアーにより、クエリ$2,3$を列に対する区間加算、$1$点取得と思えるがこれはBITで可能。
コード
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
#include "data_structure/union-find.hpp"
#include "template.hpp"
#include <atcoder/fenwicktree>
struct query {
ll t, a, b;
ll id;
};
void solve() {
LL(n, q);
vl p(2 * n - 1);
iota(all(p), 0);
vll c(2 * n - 1);
vector<query> vq(q);
ll aux = n;
UnionFind uf(n);
auto merge = [&](ll a, ll b) {
a = uf.leader(a), b = uf.leader(b);
if(a == b)
return;
c[aux].push_back(p[a]);
c[aux].push_back(p[b]);
p[uf.merge(a, b)] = aux++;
};
rep(i, q) {
LL(t, a, b);
--a;
if(t == 1) {
b--;
merge(a, b);
}
vq[i] = query(t, a, b, p[uf.leader(a)]);
}
rep(i, 1, n) merge(0, i);
atcoder::fenwick_tree<ll> fw(n + 1);
vl in(2 * n - 1), out(2 * n - 1);
ll time = 0;
auto dfs = [&](auto &&dfs, ll cur) -> void {
in[cur] = time;
if(cur < n)
time++;
for(auto nex : c[cur])
dfs(dfs, nex);
out[cur] = time;
};
dfs(dfs, 2 * n - 2);
for(auto qi : vq) {
if(qi.t == 1)
continue;
else if(qi.t == 2) {
ll idx = qi.id;
fw.add(in[idx], qi.b);
fw.add(out[idx], -qi.b);
} else {
print(fw.sum(0, in[qi.a] + 1));
}
}
}
int main() {
ios::sync_with_stdio(false);
std::cin.tie(nullptr);
solve();
}
他の問題
ここに解説とコードのリンクがある
トップダウンに和を取る
LCAを使う
$K$についての制約を除いた問題が、マージ過程を表す木を考えることにより部分木についてのクエリに帰着できる。解説を参照せよ。
参考
Union Sets https://t.co/phnbNZyz3T
— SSRS (@SSRS_cp) November 25, 2021
Union add query (想定ではない) https://t.co/fnTr1KoxvC
Black Cats Deployment https://t.co/vJMJcA4XfV
Graph and Queries https://t.co/5SBgU8Xhe2